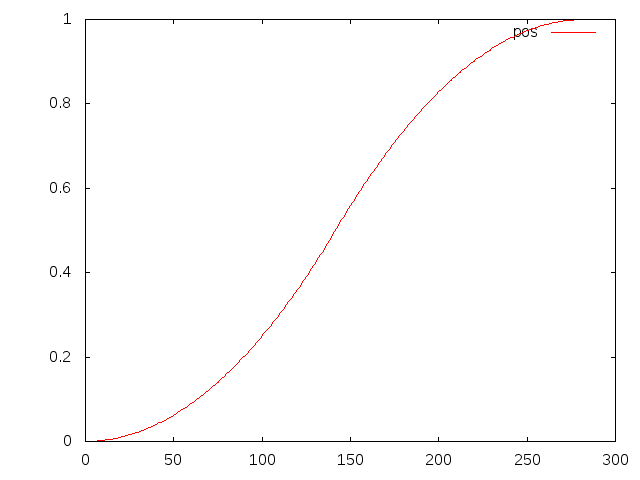
example 1 input position
It is built on the TAO dynamics engine which allows to compute forward kinematics as well as forward and inverse dynamics of branching structures mode of rigid bodies connected via revolute or prismatic joints.
The best place to start browsing the joint-space documentation is jspace::Model which is the high-level facade that ties it all together.
The trajectory is stored in a text file where each line consists of 2N numbers: the first N numbers are the joint positions, and the second set of N numbers are the joint velocities. Each line represents a sample in time, and the samples are regularly spaced with a fixed timestep.
The robot description is in an XML file that specifies the links and joints, the coordinate frame transformations between them, and their masses and inertias.
The trjsim takes that XML robot file, constructs a jspace::Model from it, and then reads in the trajectory one line at a time. For each sample, it calls jspace::update() with the current state, computes the acceleration required to get to the next sample, and uses the information from jspace::Model::getMassInertia() and jspace::Model::getGravity() in order to compute the torques. It then writes out the positions, velocities, acceleration, as well as the torque with and without gravity compensation.
Once the trajectory file has been completely processed, trjsim prints out a little help text in case you want to plot the result with gnuplot.
$ cd build/jspace/applications $ ./trjsim -s ../../../jspace/examples/unit-mass-pz.xml -i ../../../jspace/examples/trj-1dof-a.txt -o result.txt
We can now look at the result in gnuplot:
$ cd build/jspace/applications $ gnuplot gnuplot> plot 'result.txt' u 0:1 w l t 'pos' gnuplot> plot 'result.txt' u 0:2 w l t 'vel' gnuplot> plot 'result.txt' u 0:3 w l t 'acc'

example 1 input position
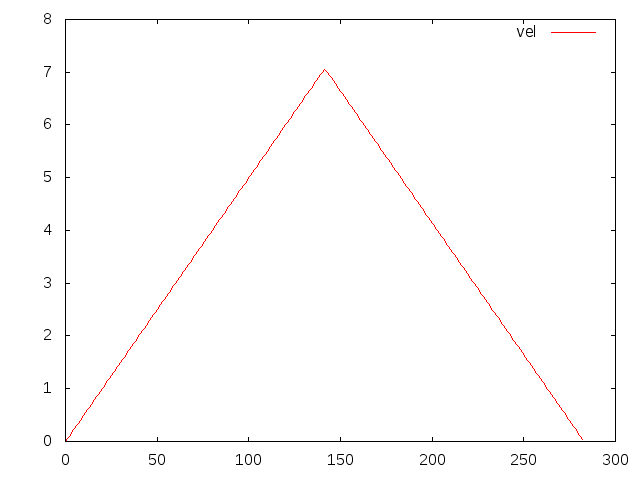
example 1 input velocity
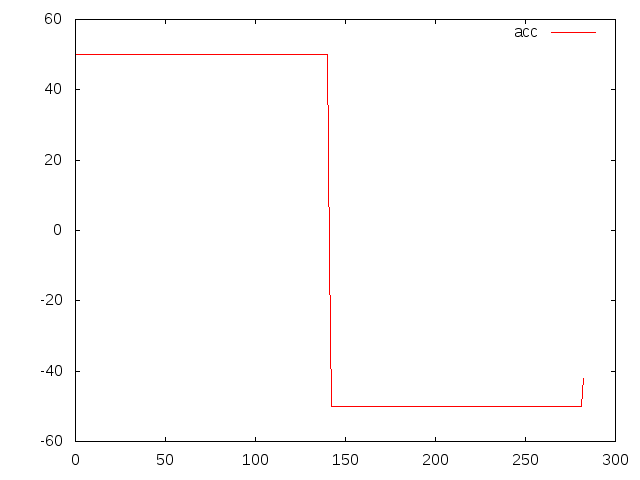
example 1 input acceleration
Let's look at the corresponding forces:
gnuplot> plot 'result.txt' u 0:4 w l t 'tau', 'result.txt' u 0:5 w l t 'tau+g'
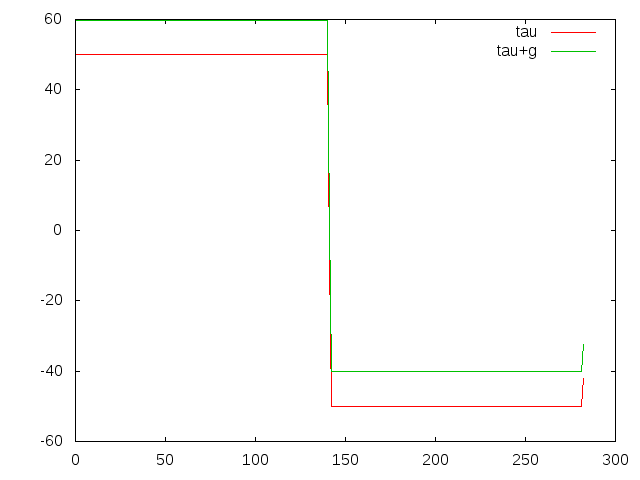
example 1 output
$ cd build/jspace/applications $ ./trjsim -s ../../../jspace/examples/unit-mass-rx-rx.xml -i ../../../jspace/examples/trj-2dof-a.txt -o result.txt
We can now look at the result in gnuplot:
$ cd build/jspace/applications $ gnuplot gnuplot> plot 'result.txt' u 0:1 w l t 'pos1', 'result.txt' u 0:2 w l t 'pos2' gnuplot> plot 'result.txt' u 0:3 w l t 'vel1', 'result.txt' u 0:4 w l t 'vel2' gnuplot> plot 'result.txt' u 0:5 w l t 'acc1', 'result.txt' u 0:6 w l t 'acc2'
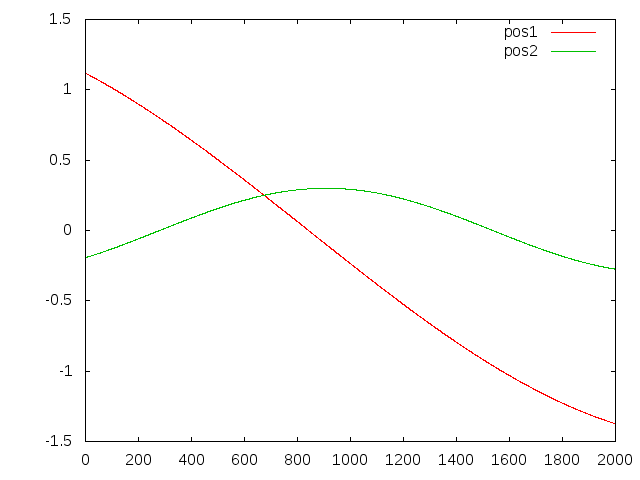
example 2 input position
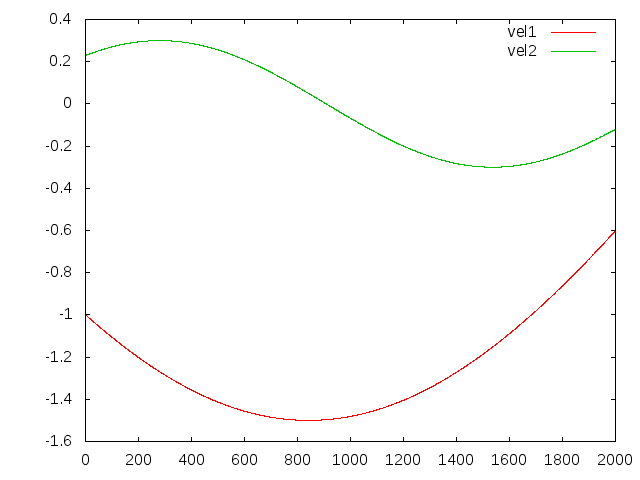
example 2 input velocity
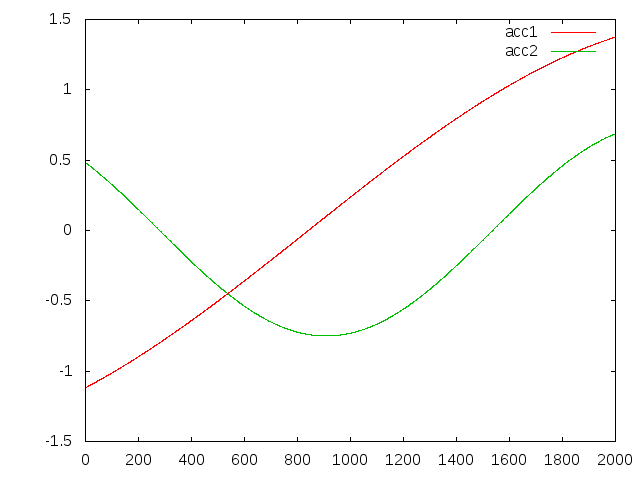
example 2 input acceleration
gnuplot> plot 'result.txt' u 0:5 w l t 'acc1', 'result.txt' u 0:7 w l t 'tau1', 'result.txt' u 0:9 w l t 'tau1+g' gnuplot> plot 'result.txt' u 0:6 w l t 'acc2', 'result.txt' u 0:8 w l t 'tau2', 'result.txt' u 0:10 w l t 'tau2+g'
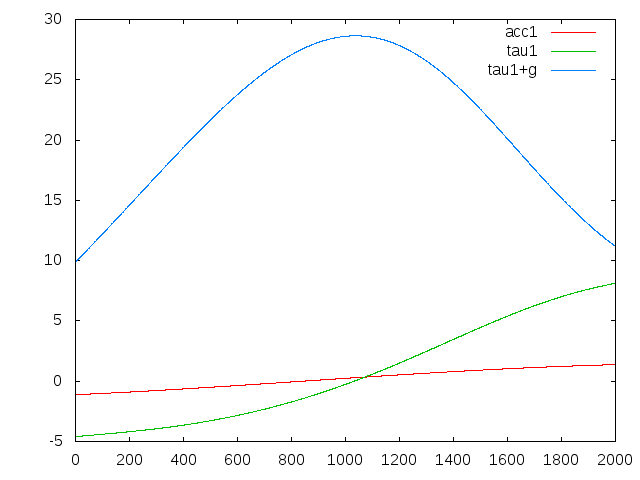
example 2 output for joint 1
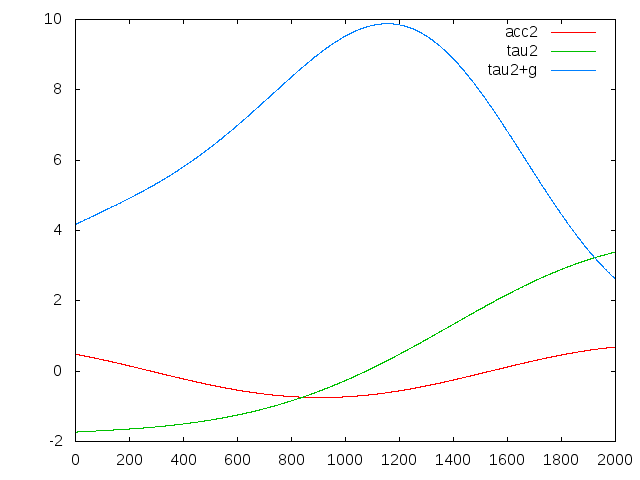
example 2 output for joint 2
 1.5.4
1.5.4